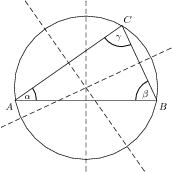
Zu jedem Dreieck \(ABC\) existiert ein Kreis, der genau durch die Eckpunkte \(A\), \(B\) und \(C\) verläuft — der so genannte Umkreis. Der Umkreismittelpunkt ist der Schnittpunkt der Mittelsenkrechten:

Anschaulich ist die Mittelsenkrechte von \(AB\) die Menge aller Punkte, die zu \(A\) und \(B\) denselben Abstand haben. Analog gilt dies für die Mittelsenkrechten von \(AC\) und \(BC\). Der Schnittpunkt aller drei Mittelsenkrechten hat also den gleichen Abstand zu \(A\), \(B\) und \(C\). Dieser Abstand ist der Radius des Umkreises:

\[\frac{BC}{2\,\sin(\alpha)}=\frac{AC}{2\,\sin(\beta)}=\frac{AB}{2\,\sin(\gamma)}.\]

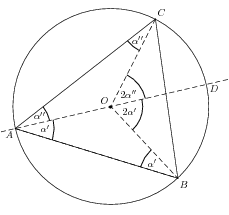
Bewiesen wird dieser Zusammenhang mit Proposition III.20 aus Euklids Die Elemente. Eine Gerade, die durch \(A\) und den Umkreismittelpunkt \(O\) verläuft, teilt \(\alpha\) in zwei Winkel \(\alpha'\) und \(\alpha''\).

Die Seiten \(AO\) und \(BO\) des entstandenen unteren Dreiecks sind gleich lang, weil sie beide Radien des Umkreises sind. Demzufolge sind die Winkel \(OAB\) und \(ABO\) gleich groß — nämlich α′. Die Summe aller Winkel im Dreieck ist 180°. Dementsprechend ist der Winkel \(AOB\) gleich 180°-2α′. Der Winkel \(BOD\) ergänzt \(AOB\) auf 180°, also muss er 2α′ groß sein. Dasselbe Argument gilt analog für α′′. Für den Winkel \(BOC\) folgt somit \[2\alpha'+2\alpha''=2(\alpha'+\alpha'')=2\alpha.\]

Mit dieser Tatsache lässt sich nun der Radius des Umkreises berechnen:

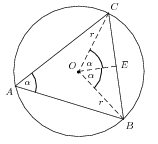
Die Mittelsenkrechte von \(BC\) erzeugt zwei gleichgroße rechtwinklige Dreiecke \(BOE\) und \(COE\). Der Winkel \(BOC\) ist 2α groß und die Mittelsenkrechte teilt diesen genau in der Hälfte. Folglich sind die Winkel \(BOE\) und \(COE\) gleich α. Analog teilt die Mittelsenkrechte auch \(BC\) genau in der Mitte:

\[CE=EB=\frac{BC}{2}.\]

In rechtwinkligen Dreiecken ist der Sinus definiert als das Verhältnis von Gegenkathete zu Hypotenuse, nämlich

\[\sin(\alpha)=\frac{\frac{BC}{2}}{r},\]

was äquivalent ist zu der vorher angegebenen Formel.